BOJ: 큰 수 연산 & A/B (시리즈)

백준의 큰 수 연산 시리즈입니다. 이상하게도 큰 수의 나눗셈이 필요한 문제는 따로 등록되어 있다. 큰 수의 연산을 해야 하는 시리즈인 만큼 함께 다루겠다. 특별히 교육적이거나 한 내용은 아니므로 심심할 때 재미 삼아 풀어보길 바란다.

 

* A+B 시리즈의 문제의 경우, 큰 수의 연산을 하기 위한 노력을 필요로 하는 문제들이 아니었으므로 다루지 않겠다.

A/B

https://www.acmicpc.net/workbook/view/6546

문제집: A/B (시리즈)

풀이

1008번: A/B

그냥 A/B를 출력한다.

 

15792번: A/B -2

정수 부분을 구해주고, 소수 부분을 따로 구해준다.

 

16428번: A/B -3

케이스를 적당히 잘 쪼개면 된다. 문제에 나온 식을 만족하는 값을 Naive 하게 찾아주면 된다.

// A/B
#include <bits/stdc++.h>
int main(){
	double A, B;
	scanf("%d %d", &A, &B);
	printf("%.9f", A/B);
	return 0;
}

# A/B -2
A,B=map(int,input().split())
ans=str(A//B)+"."
A=A%B*10
for i in range(1200):
    ans+=str(A//B)
    A=A%B*10
print(ans)

# A/B -3
A,B=map(int,input().split())
x=A//B
while A-B*x<0:
    if B<0:x+=1
    else:x-=1
print(x)
print(A-B*x)

 

큰 수 연산

https://www.acmicpc.net/workbook/view/6565

문제집: 큰 수 연산 (시리즈)

풀이

10757번: 큰 수 A+B

그냥 python 쓰자.

 

15353번: 큰 수 A+B (2)

배열을 가지고 덧셈을 해준다. 자리 올림에 신경 쓰도록 하자.

 

13277번: 큰 수 곱셈

이것도 그냥 python 쓰자.

 

15576번: 큰 수 곱셈 (2)

숫자를 아래와 같이 다항식으로 표현하자. 다항식 곱셈은 FFT를 통해 빠르게 할 수 있다.

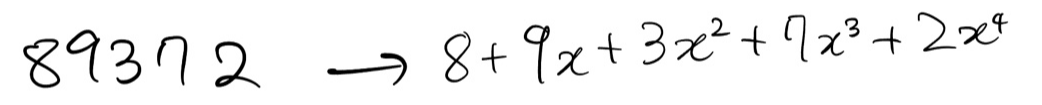
# 큰 수 A+B
a,b=map(int,input().split())
print(a+b)

# 큰 수 곱셈
a,b=map(int,input().split())
print(a*b)

// 큰 수 A+B (2)
#include <bits/stdc++.h>
using namespace std;
char S[10003],T[10003];
int main(){
    scanf("%s %s",S,T);
    int ss=strlen(S)-1,tt=strlen(T)-1;
    stack<int>ans;int k=0;
    while(ss>=0&&tt>=0){
        int tmp=S[ss]+T[tt]-2*'0'+k;k=tmp/10;
        ans.push(tmp%10);
        ss--;tt--;
    }
    while(ss>=0){
        int tmp=S[ss]-'0'+k;k=tmp/10;
        ans.push(tmp%10);
        ss--;
    }
    while(tt>=0){
        int tmp=T[tt]-'0'+k;k=tmp/10;
        ans.push(tmp%10);
        tt--;
    }
    if(k)ans.push(k);
    while(!ans.empty()){
        printf("%d",ans.top());
        ans.pop();
    }
    return 0;
}

// 큰 수 곱셈 (2)
// Written by Haruki Fukuhisa
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
using lf=double;
const ll N=(1<<20);
const lf pi=3.141592653589793238;
void FFT(complex<lf> *a,bool f){
    ll i,j=0,k;
    for(i=1;i<N;i++){
        for(k=N>>1;k<=j;k>>=1)j-=k;
        j+=k;
        if(i<j)swap(a[i],a[j]);
    }
    for(i=1;i<N;i<<=1){
        double phi=2*pi/(i<<1)*(f?(-1):1);
        complex<lf>x(cos(phi),sin(phi));
        for(j=0;j<N;j+=i<<1){
            complex<lf>y(1);
            for(k=0;k<i;k++){
                complex<lf>z=a[i|j|k]*y;
                a[i|j|k]=a[j|k]-z;
                a[j|k]+=z;
                y*=x;
            }
        }
    }
    if(f){
        for(i=0;i<N;i++)a[i]/=N;
    }
}
complex<lf>X[N],Y[N];
char S[300004],T[3000003];
ll ans[N];
int main(){
    scanf("%s %s",S,T);
    int ss=strlen(S),tt=strlen(T);
    for(int i=0;i<ss;i++){
        X[i]=S[i]-'0';
    }
    for(int i=0;i<tt;i++)Y[i]=T[i]-'0';
    FFT(X,false);FFT(Y,false);
    for(int i=0;i<N;i++){
        X[i]*=Y[i];
    }
    FFT(X,true);
    int E=ss+tt-1;
    ll pp=0;
    for(int i=0;i<E;i++){
        ans[i]=(X[i].real()+(X[i].real()>0?0.5:-0.5));
    }
    for(int i=E-1;i>0;i--){
        if(ans[i]>=10){
            if(i<=0)pp=ans[i]/10;else ans[i-1]+=ans[i]/10;
            ans[i]%=10;
        }
    }
    if(pp)printf("%lld",pp);
    for(int i=0;i<E;i++){
        printf("%lld",ans[i]);
    }
    return 0;
}